Драбина (теорія графів)

Ladder graph
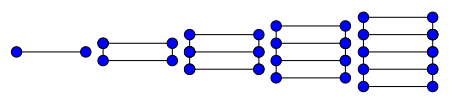
Граф драбина L8.
Вершин	2n
Ребер	3n-2
Хроматичне число	2
Хроматичний індекс	3 для n>2 2 для n=2 1 для n=1
Властивості	одиничних відстаней гамільтонів планарний двочастковий
Позначення	Ln

В теорії графів драбина L_n — планарний неорієнтований граф з 2n вершинами і n+2(n-1) ребрами .

Драбину можна отримати прямим добутком двох шляхів, один з яких має тільки одне ребро — L_n,1 = P_n × P₁ . Якщо додати ще два ребра, що перетинаються і з'єднують чотири вершини драбини зі степенем два, одержимо кубічний граф — драбину Мебіуса.

З побудови, драбина L_n ізоморфна решітці G_2,n і виглядає як драбина з n щаблями. Граф є гамільтоновим з охопленням 4 (якщо n>1) і хроматичним індексом 3 (якщо n>2).

Хроматичне число драбини дорівнює 2, а її хроматичний многочлен дорівнює $(x-1)x(x^{2}-3x+3)^{(n-1)}$.

Кільцевий драбинний граф

Кільцевий драбинний граф CL_n — це прямий добуток циклу довжини n≥3 і ребра. В символьному вигляді CL_n = C_n × P₁. Граф має 2n вершин і 3n ребер. Подібно до драбини граф є зв'язним, планарним і гамільтоновим, але граф є двочастковим тоді й лише тоді, коли n парне.

Кільцевий драбинний граф — це багатогранний граф призм, тому його частіше називають графом призми.

Кільцеві драбинні графи:

CL3

CL4

CL5

CL6

CL7

CL8

Драбина Мебіуса

З'єднавши чотири вершини степеня 2 «навхрест», отримаємо кубічний граф, який називають драбиною Мебіуса.

Два вигляди драбини МебіусаM₁₆ .

Галерея

Драбини L₁, L₂, L₃, L₄ і L₅.

• 
  Хроматичне число драбини дорівнює 2.

Література

• H. Hosoya, F. Harary. On the Matching Properties of Three Fence Graphs // J. Math. Chem.. — 1993. — Вип. 12 (11 листопада). — С. 211-218.
• M. Noy, A. Ribó. Recursively Constructible Families of Graphs // Adv. Appl. Math. — 2004. — Вип. 32 (11 листопада). — С. 350-363.
• Yichao Chen, Jonathan L. Gross, Toufik Mansour. Total Embedding Distributions of Circular Ladders // Journal of Graph Theory. — 2013. — Т. 74, вип. 1 (1 вересня). — С. 32–57. — DOI:10.1002/jgt.21690.